Linear Least Squares
“An approximate answer to the right problem is worth a good deal more than an exact answer to an approximate problem.” - John Tukey
Preamble
Lagrange multipliers
We have a function $a$ -> $f(x,y)$ and an equation $b$ -> $x^2 + y^2 = 1$. We want values of $x$ and $y$ that satisfies both, and that results in a subset of the $x,y$ plane that satisfies the equation. With our example, that would mean that the only $x,y$ values we want are the ones that satisfy the equation: $x^2 + y^2 = 1$.
Not only do we want to find a, we may want to find a subset that optimises the value of $a$. We may want to find the minima of $a$, or the maxima.
Now note that the contour lines indicates the boundaries of different values for $f(x,y)$ and $b(x,y)$, and if you wanted to change values the fastest,a straight perpendicular line between the curves does the job (obviously, since it’s the gradient). Hence the gradients of $a$ and $b$ will be perpendicular at the point indicated.
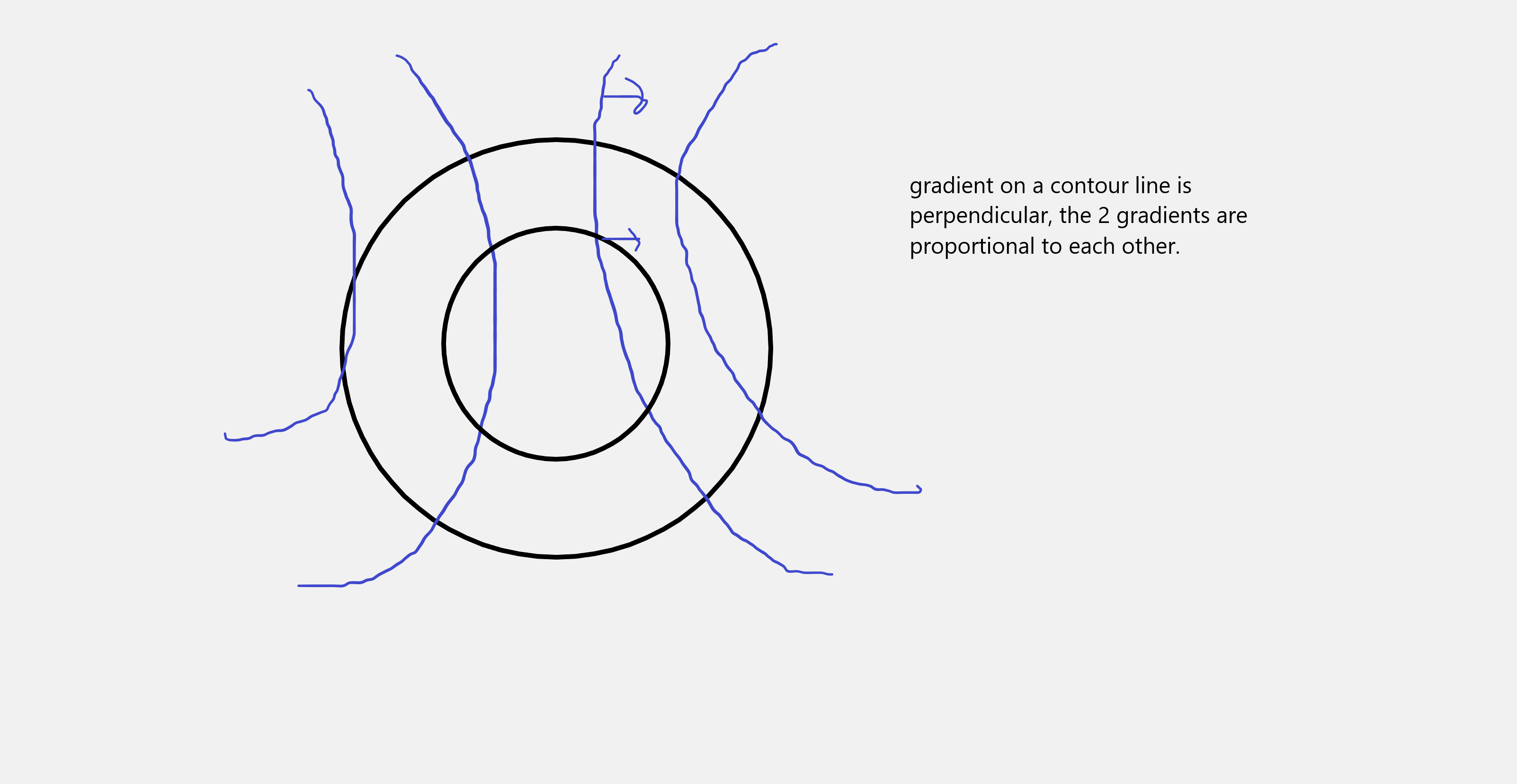
The gradient of $b$ will point in the direction as the gradient of $f$, and they will not necessarily be equal but proportional to each other: \(\partial _{x,y} a = \lambda \partial _{x,y} b\)
So we have 2 equations, and we add a third equation which is the constraint itself:
Then we solve the system of equations with the lagrangian: $L(x, y, \lambda) = f(x,y) - \lambda(b(x,y) - const)$
When we take the gradient of that lagrangian function above and set it to 0 as in: $\partial _{x,y, \lambda}L$, we have the 3 equations packed together.
Linear Least Squares
Problem: $Ax = b$
$Ax$ is a linear combination of the vectors in $A$ that results in a vector $b$, we have the matrix, we have $b$ and we want to find $x$, but sometimes we can’t get the exact solution, so we want to get very close to the correct answer i.e the most correct $x$ that $A$ transforms to $b$, but in what instances can’t we get the exact solution? We cannot get the exact solution when the matrix is a subspace of the space $b$ lives in, thus the rank of $A$ is not maximal.
Assuming $A$ is a $n \times p$ matrix, when $n < p$,then there are multiple solutions.
We can rewrite the above problem as: $Ax-b = 0$
So $Ax-b$ is a vector, and we want to minmise it’s length, how do we deal with vector lengths? Ans = dot/inner products.
If $b = 0$, then $Ax = 0$ and a solution is $x = 0$, but we do not want that trivial solution, so we need to place a constraint on our equation.
Hence we want to minimise $\lVert Ax \rVert$ if $b = 0$ and $\lVert Ax-b \rVert$ if $b != 0$
Let’s tackle the case where $b = 0$ and we want to minimise $\lVert Ax \rVert$ s.t a constraint on $x$.
We have to make a minor modification though, because we calculate norms with dot products. $\lVert Ax \rVert$ = $\sqrt{(Ax \cdot Ax)} = \sqrt{(A{x}^TAx)}$, but this function is undefined at $x = 0$ and thus not differentiable at that point. We know that for minimization purposes we need it to be differentiable everywhere.
So instead we minimise ${\lVert Ax \rVert}^2 = A{x}^TAx$, which is a smooth function and gives us the same results (gives us the same results because it is a monotonic order preserving transformation i.e if $x>y$ then $f(x) > f(y)$.
Now we simplify ${Ax}^TAx$, and obtain ${x}^T{A}^TAx$.
Looks like we have gotten an optimisation problem where we have to minimise a quadratic form subject to a constraint.
=> minimize ${x}^T{A}^TAx$ st the condition that $\lVert x \rVert = 1$
=> minimize ${x}^T{A}^TAx$ st the condition that ${x}^Tx = 1$
This constrained optimization problem can be solved with Lagrange multipliers. As explained above, we end up having to minimize: ${x}^T{A}^TAx + \lambda({x}Tx-1)$
Take derivatives of the lagrangian with respect to $x$ and we get:
${A}^TAx + \lambda x = 0$.
The equation derived from the $x$ partial derivative: ${A}^TAx + \lambda x = 0$ indicates that $x$ is an eigenvector of ${A}^TA$ with eigenvalue $-\lambda$.
By setting the derivative with respect to $\lambda$ to zero, we enforce the constraint on the solution, ensuring that minimization is performed within the feasible set defined by the constraint ∥𝑥∥=1
Our goal was to minimize ${x}^T{A}^TAx$, so we need the eigenvector $x$ with the smallest eigenvalue. The matrix ${A}^TA$ was thus decomposed into eigenvalues and eigenvectors.
Now let’s move on to the case where we want to minimise $\lVert Ax - b \rVert$ for a nonzero $b$. Like above we would minimise $ {\lVert Ax - b \rVert} ^2$, but we do not need a constraint as we can’t get a trivial solution of $0$…and we also do not need lagrange multipliers since we are not optimising with respect to a constraint.
${\lVert Ax - b \rVert}^2 $ = ${(Ax−b)}^TAx−b = {x}^T{A}^TAx−2{b}^TAx+{b}^Tb$.
Take partial derivatives of the function and set them to $0$ (to find the minimum), then we get
=> $2{A}^TAx−2{A}^Tb=0$.
=> ${A}^TAx - {A}^Tb = 0$.
Hence ${A}^T (Ax - b) = 0$ => $A \cdot (Ax-b)$ = 0
Thus $A$ is orthogonal to $Ax - b$
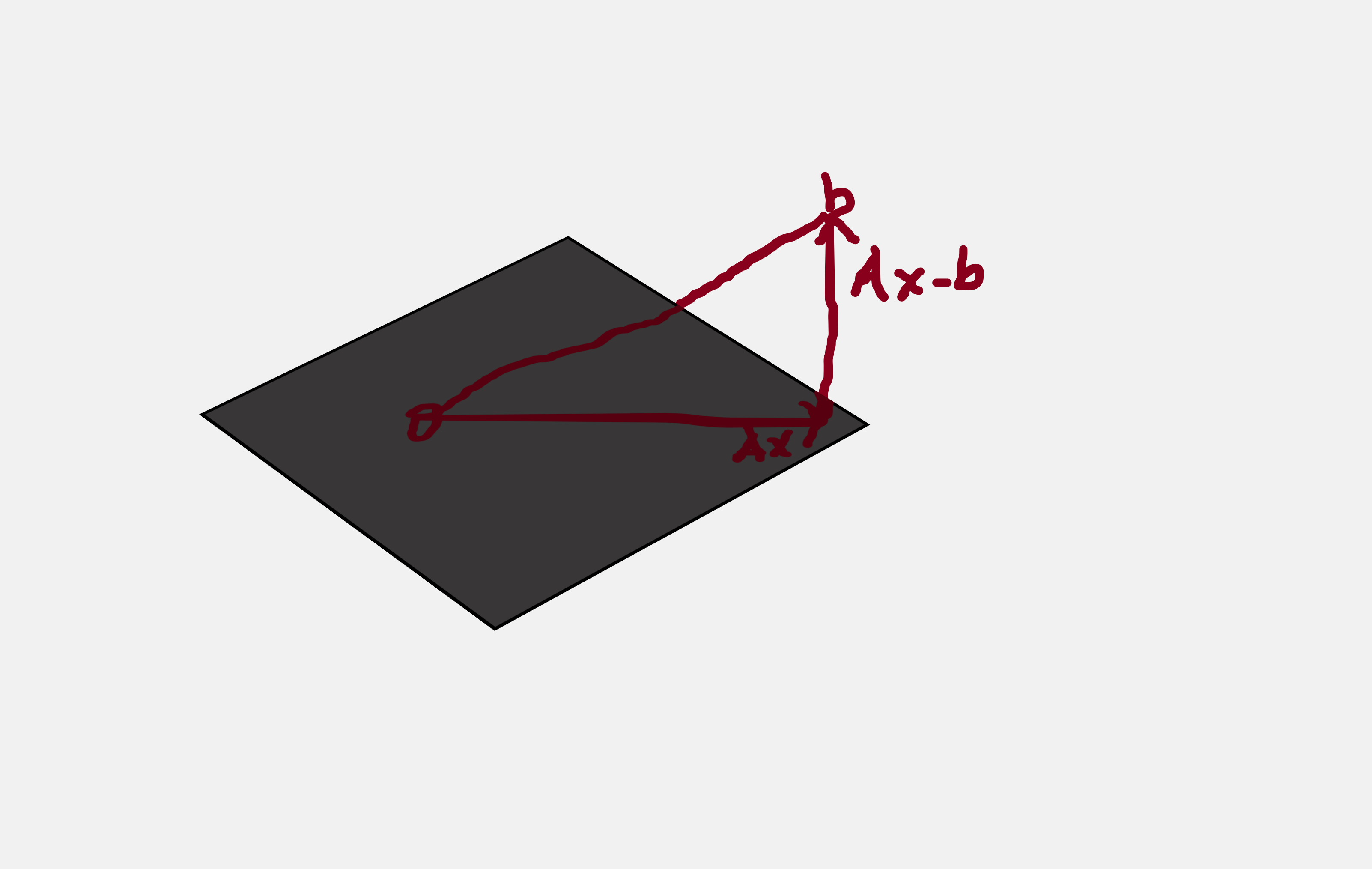
If the span of A defines a plane, then it means that Ax - b is orthogonal to the plane.
$x = {({A}^TA)}^{−1}A^Tb$. (Note that $A$ has to be invertible)