Mild thoughts on Projective Geometry

“No man ever steps in the same river twice, for it’s not the same river and he’s not the same man.” - Heraclitus

“When an object is transformed, we observe a change in it. However, does any property of the object truly change, or is it our perception of the object that changes?”. I believe the question of perception and change lends key insight into the nature of geometry and projective equivalence.

My view of projective geometry exists in two forms, the first of which is more formal than the second:

• The study of properties that are invariant under projective transformation.
• The view of objects through a higher-dimensional lens.

The Study of Invariant Properties under Projective Transformation

We can accurately capture the essence of abstraction in mathematics, illustrating how specific operations and entities in arithmetic and geometry are generalized into the broader frameworks of algebra and geometry. This abstraction allows mathematicians to study more complex and general properties beyond specific instances. In this context, you have a group of objects that follow a specific rule, and you define an operation on the members of that group based on the premise that the members obey the laws that define the structure of the group.

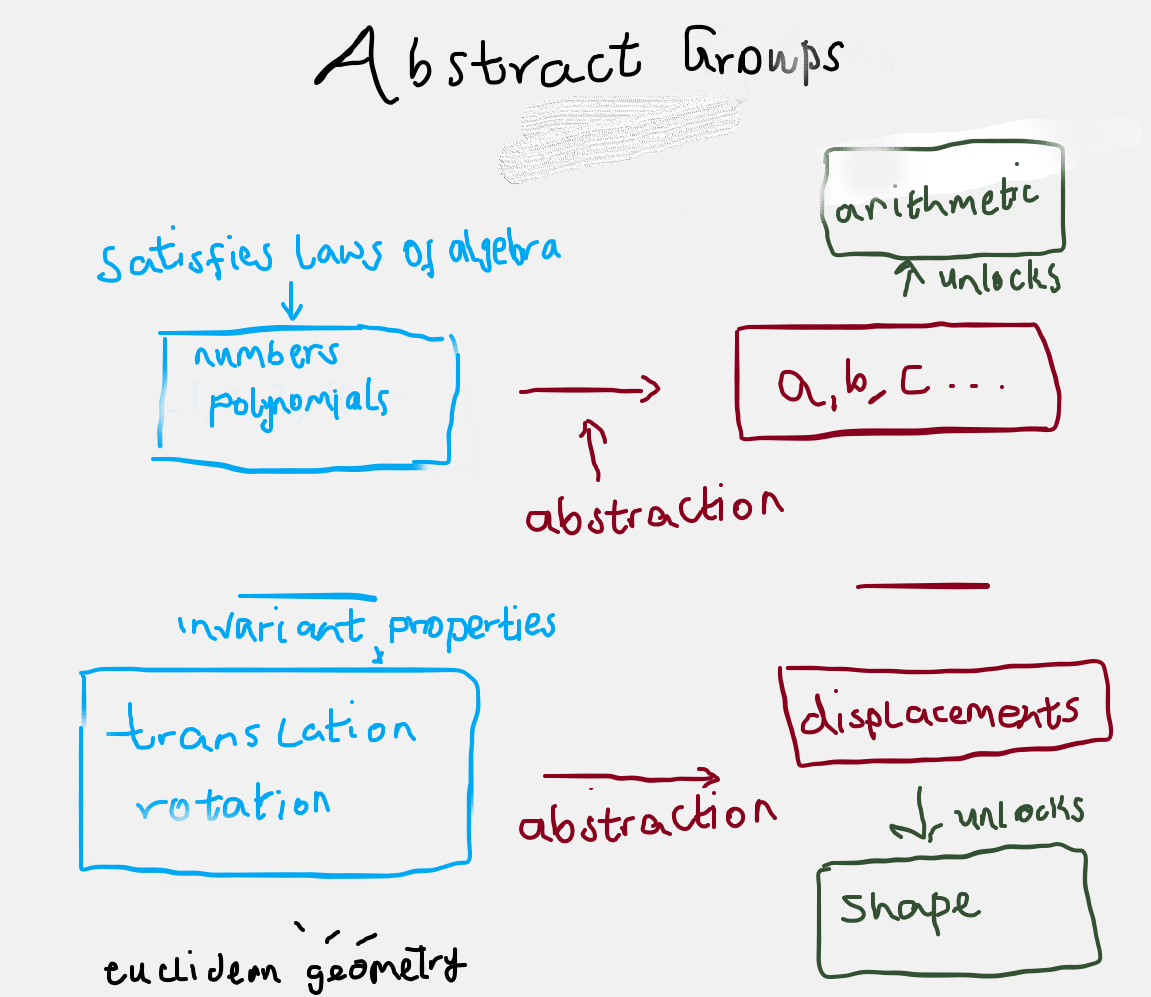
Taking a cue from Kneebone’s ‘Algebraic Projective Geometry’, we see that if numbers and polynomials both satisfy the laws of algebra, then they share a common structure, and we may study a system based on that structure without going into the specifics of the nature of the objects involved other than the fact that they all possess the structure in question.
This relates to the ideas in Linear Algebra, where vectors can be of different forms, or live in different spaces. Polynomials, real numbers, and geometric objects are different objects, but they share the fundamental structure that defines linear algebra - vectors. Even though we can intuit one from the other (e.g dot products -> inner products), we do not need to project the properties of one onto the other. Thus, when we talk about the “length of a polynomial” via inner products for example, we are taking a view from the geometric vector space.

Now, in Euclidean geometry, rotations and scalings, for example, have a common spatial structure - they both preserve shape. Generally speaking, displacements possess a common spatial structure. A translated, rotated square is considered to be the same square, i.e., the shape is invariant. Euclidean geometry is thus the invariant theory of the group of displacements, and based on these invariants, we define a metric—a way to measure distances, angles, and other structural aspects of the geometry. In a way, these operations define a space, as the Euclidean transformations limit you to the Euclidean space. The same analogy can be carried over to projective geometry, which we define as the invariant theory of the group of projections. That is, under projective transformations, find out which properties of the object remain invariant, and then we define a metric based on those properties.

The view of objects through a higher-dimensional lens

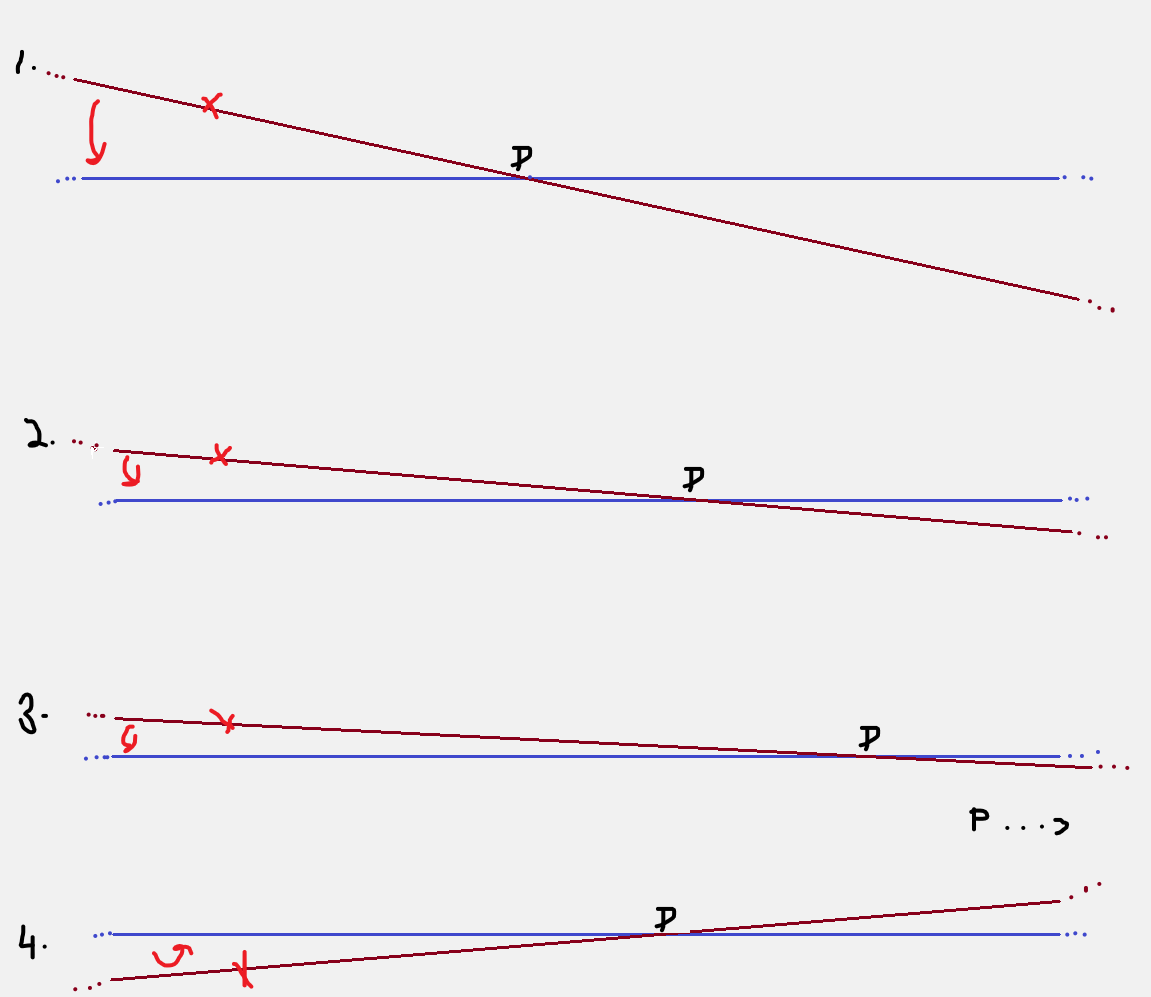
On first contact, the statement: “Parallel lines meet at a point in infinity” seems rather absurd, but observing the image above, we see 2 lines (treat these as lines with no limitations on length), and we observe that with a rotation of the red line about the point “x”, the point of intersection of the two lines “p”, moves further and further along the blue line, and as the red line gets closer to being parallel with the blue line, it appears to be that the point “p” approaches an “infinite” point along that blue line.
Considering the oft-used “railway tracks” example, we consider the fact that those lines live on a plane, and we live in 3D space, this means that we have the liberty and freedom of an extra dimension, this extra dimension offers insight through a different view of the same object. The parallelism of the two lines says nothing about the 3D space in which they live, but the 3D space is in no way compelled to say nothing about the 2D objects in its purview.
I plan to discuss more on this and the concept of projective equivalence in a follow-up post.

References

• Hartley, R., & Zisserman, A. (2004). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge: Cambridge University Press.

• Kneebone, G. T. (1960). Algebraic Projective Geometry. Oxford: Clarendon Press.